Кодирующая обезьянка

Дельта робот относится к так называемым параллельным роботам. В станках с ЧПУ, рабочие органы которых движутся по линейным направляющим в X, Y и Z плоскостях, которые жестко закреплены под 90° друг к другу. Дельта робот же построен на треугольниках и параллелограммах. Дельта робот и его кинематека

Когда поток жидкости или газа обтекает цилиндрические тела, с таких тел поочередно начинают срываться вихри. Причем их вращение противоположно, и, срываясь, они поддерживают друг друга. Этот эффект называется дорожка Кармана. Вихревая дорожка Кармана Вихревая дорожка характерна не только для цилиндрических тел. С ней стараются бороться, так как вибрации, создаваемые вихрями, могут разрушительно воздействовать на сам объект. Но иногда этот эффект можно использовать и во благо.

Улыбающийся человек на фотографии Карл Раймунд Поппер. Австрийский ученый, философ активно критиковал существующие на то время понятия о научном методе, занимался проблемой демаркации знаний. И в 1935 году сформулировал критерий "научности" или "антинаучности" любой теории или гипотезы. Этим критерием является фальсифицируемость или "критерий Поппера" .

Кратчайший путь между двумя точками на поверхности Земли можно найти с помощью ортодромии . Именно так, если нет никаких дополнительных факторов (например погода, течения), стараются прокладывать маршрут для самолетов и кораблей. Ортодромия

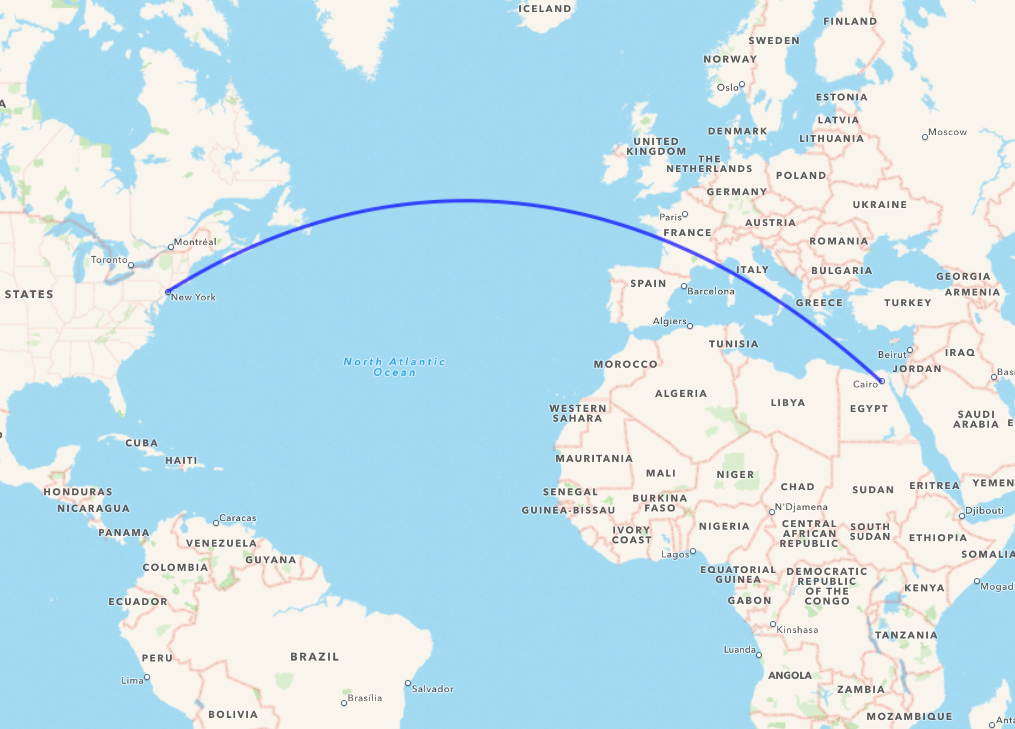
Какой кратчайший путь между двумя точками? Казалось бы, глупый вопрос. Со школы мы знаем, что кратчайшее расстояние между двумя точками на плоскости - прямая, отсюда:  `L = sqrt( (x_1-x_2)^2 + (y_1-y_2)^2 )` Ключевое слово здесь плоскость. Если поверхность вогнутая или выпуклая (например, поверхность земного шара), то приходится считаться с этой кривизной. Если мы прокладываем путь на карте и расстояние невелико (например, десятки километров), а точки находятся вблизи экватора, то можно считать, что земля на этом участке "плоская" и пренебречь ее формой. Это значительно упрощает расчеты: соединил две точки прямой при помощи линейки и всё. Погрешность при этом будет невелика. С увеличением расстояний кривизна земли все больше и больше влияет на конечный результат. И если необходимо провести действительно наикратчайший маршрут между двумя точками на Земле, то тут в игру вступает ортодромия: Вот так выглядит самый короткий путь